Синус. Тайник

Вот пара чисел:

0,7420219

0,5749783

Всего лишь одно математическое действие, как-то связанное с названием тайника и числа превратятся в координаты тайника! Ну, еще может надо придать координатам привычный вид. По полученным координатам, которые можно проверить – дерево с дуплом возле дороги и реки. А координаты в заглавии – приблизительные.

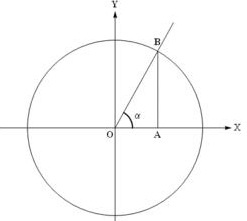
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим x_B, ординату обозначим y_B (см. рисунок).

Синусом называется отношение sinα=y_B/R

 Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера. Сам термин тригонометрические функции введён Клюгелем в 1770 году.

Источник